Two-wheeled Inverted Pendulum Dynamics

The TWIP is by construction an inverted pendulum that is no longer fixed at a single point. While fairly easy to design an implement, analysis of this system leads to a set of coupled non-linear equations. Notably, the principles behind the TWIP are present in a large number of other systems (Rockets, Bipedal, Segways). As a result, designing an efficient controller for this system has been an active area of research. However, the TWIP belongs to a set of underactuated robots, which implies that it is inherently unstable (without an active controller) and coupled with the non-intuitive nature of the dynamics, it is a challenge to design a robust controller.

The analysis of the TWIP can begin with a simple free body diagram.

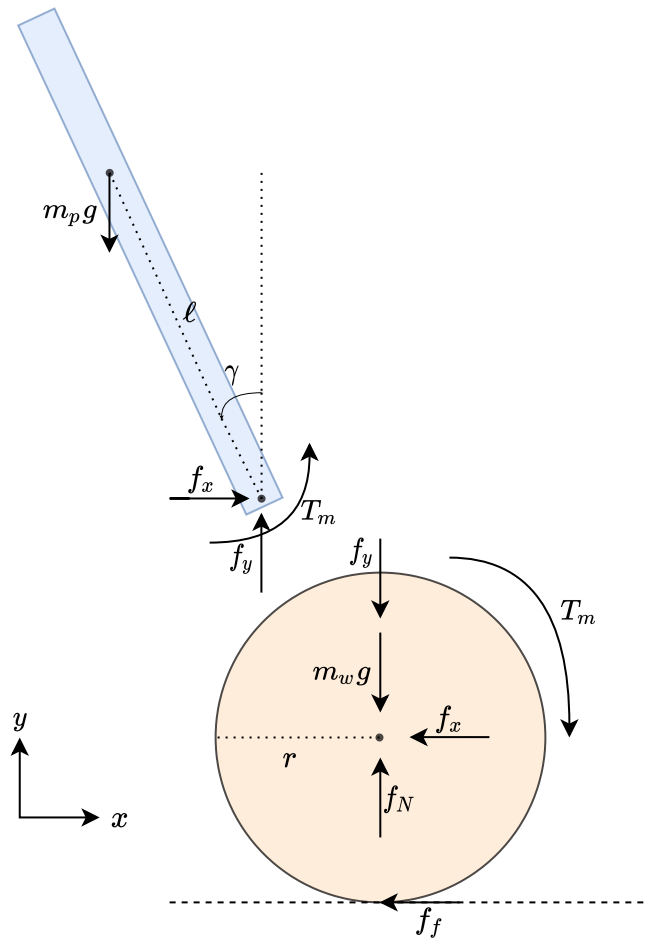
The system can be analyzed in 2D to simplify the problem slightly. Analyze each component (body & wheel) separately. Equations for each Wheel

\[\begin{align} \ddot{x}m_{w} &= f_{f} - f_{x}\\ \ddot{y}m_{w} &= f_N - f_y - m_{w}g = 0\\ I_{w}\ddot{\psi} &= -f_{f}r + T_{m} \end{align}\]

Equations for pole

\[\begin{align} \ddot{x}_{p}m_{p} &= 2f_{x}\\ \ddot{y}_{p}m_{p} &= 2f_y - m_{p}g = 0\\ I_{p}\ddot{\gamma} &= 2 f_{y}\ell \sin(\gamma) -2 f_{x}\ell \cos(\gamma) + 2T_{m} \end{align}\]

The relationship between wheel rotation (\(\psi\)) and wheel linear displacement (\(x\)) is \(\begin{align} x &=\psi r\\ \dot{x} &=\dot{\psi}r\\ \ddot{x} &=\ddot{\psi}r \end{align}\)

The center of gravity is displaced as governed by \(\begin{align} x_{p} &= x - \ell\sin(\gamma)\\ y_{p} &= \ell\cos(\gamma) \end{align}\)

Taking time derivatives, \(\begin{align} \dot{x}_{p} &= \dot{x} - \dot{\gamma}\ell\cos(\gamma)\\ \ddot{x}_{p} &=\ddot{x} -\ell\ddot{\gamma}\cos(\gamma)+\ell\dot{\gamma}^2\sin(\gamma)\\ \dot{y}_{p} &= -\dot{\gamma}\ell\sin(\gamma)\\ \ddot{y}_{p} &= -\ell\ddot{\gamma}\sin(\gamma)-\ell\dot{\gamma}^2\cos(\gamma \end{align}\)

Simplifying a little … \(\begin{align} I_{p}\ddot{\gamma} &= m_p g\ell \sin(\gamma) - \ddot{x}_{p}m_{p}\ell \cos(\gamma) +2T_{m}\\ &= m_p g\ell \sin(\gamma) - (\ddot{x}-\ell\ddot{\gamma}\cos(\gamma)+\ell\dot{\gamma}^2\sin(\gamma))m_{p}\ell \cos(\gamma) +2T_{m}\\ I_{p}\ddot{\gamma} &=2 T_m + m_p g\ell \sin(\gamma) - \ddot{x} m_{p}\ell \cos(\gamma)\\ &+m_{p}\ell^2\ddot{\gamma}\cos^2(\gamma) -m_{p}\ell^2\dot{\gamma}^2\sin(\gamma)\cos(\gamma) \end{align}\)

Simplifying further … \(\begin{align} I_{w}\ddot{\psi} &= -(\ddot{x}m_{w} + f_{x}) r + T_{m}\\ I_{w}\ddot{\psi} &= -(\ddot{x}m_{w} + \dfrac{\ddot{x}_{p}m_{p}}{2}) r + T_{m}\\ I_{w}\dfrac{\ddot{x}}{r} &= -\ddot{x}m_{w}r -\ddot{x}_{p}\dfrac{m_{p}r}{2} + T_{m}\\ I_{w}\dfrac{\ddot{x}}{r} &= -\ddot{x}m_{w}r -(\ddot{x}-\ell\ddot{\gamma}\cos(\gamma)+\ell\dot{\gamma}^2\sin(\gamma))\dfrac{m_{p}r}{2} + T_{m}\\ I_w\ddot{x} &=T_m r - \ddot{x}m_{w}r^2 - \ddot{x} \dfrac{m_{p}r^2}{2} - \ell\dot{\gamma}^2\sin(\gamma)\dfrac{m_{p}r^2}{2} +\ell\ddot{\gamma}\cos(\gamma) \dfrac{m_{p}r^2}{2}\\ I_w\ddot{x} &=T_m r - (m_{w} + \dfrac{m_{p}}{2})\ddot{x}r^2 - \left[\dot{\gamma}^2\sin(\gamma) - \ddot{\gamma}\cos(\gamma)\right]\dfrac{m_{p}\ell r^2}{2} \end{align}\)

To understand how the torque \(T_m\) is generated, consider the circuit below

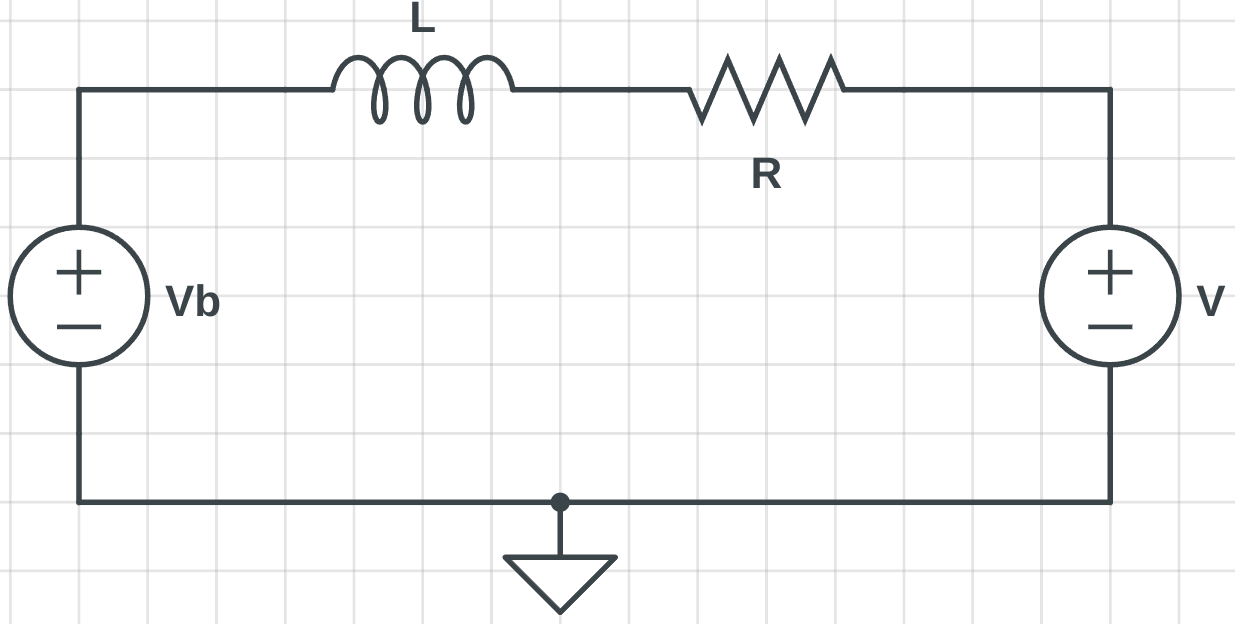
As the motor rotates, a potential (\(V_b\)) is induced which is equal to \(V_b = K_e \dot{\psi}\), where \(K_e\) is the emf constant. The motor torque is equal to \(T = K_t i\), where \(K_t\) is the motor torque constant. Solving for the steady state torque,

\[\begin{align} i &= \dfrac{V - V_b}{R} = \dfrac{V - K_e \dot{\psi}}{R}\\ T &= K_t\dfrac{V - K_e \dot{\psi}}{R} \end{align}\]

To obtain the torque \(T_m\), damping be considered. The final torque generated is \(T_m =\dfrac{K_t}{R}(V - K_e \dot{\psi}) - b \dot{\psi}\) Note, it is assumed the moment of inertia of the motor shaft is negligible when compared to the wheel.

Finally, the analysis above results in the following two equations

\[\begin{align} \ddot{x} &= \dfrac{\left[\dfrac{K_t}{R}(V - K_e \dot{\psi}) - b \dot{\psi} \right] r - \left[\dot{\gamma}^2\sin(\gamma) - \ddot{\gamma}\cos(\gamma)\right]\dfrac{m_{p}\ell r^2}{2}}{\left[I_w + (m_{w} + \dfrac{m_{p}}{2}) r^2\right]}\\ \ddot{\gamma} &= \dfrac{2 \left[ \dfrac{K_t}{R}(V - K_e \dot{\psi}) - b \dot{\psi} \right] + m_p g\ell \sin(\gamma) - \ddot{x} m_{p}\ell \cos(\gamma)+m_{p}\ell^2\ddot{\gamma}\cos^2(\gamma) -m_{p}\ell^2\dot{\gamma}^2\sin(\gamma)\cos(\gamma)}{I_p} \end{align}\]